

I was working on some continued fractions, and came across the fundamental recurrence formula above. It worked pretty well for some simple continued fractions (like √2) but seemed to be a bit unfriendly towards calculating π.
I'm using this definition of π:
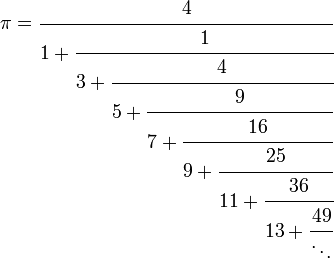
Now, using that definition with the above equation, it was always completely wrong...
So I tried changing the equation...
I'm using this definition of π:

Now, using that definition with the above equation, it was always completely wrong...
So I tried changing the equation...
 So you'll notice a few specific changes... 1) A1 has been redefined in terms of previous results. 2) A1 reduced the index on a1 to a0. 3) An+1 changed the index on an+1 to an. 4) Bn+1 changed the index on bn+1 to bn.
So you'll notice a few specific changes... 1) A1 has been redefined in terms of previous results. 2) A1 reduced the index on a1 to a0. 3) An+1 changed the index on an+1 to an. 4) Bn+1 changed the index on bn+1 to bn.This may seem like a lot of changes, but really #1 didn't change the outcome at all and the rest were all about reducing the index of a/b.
Net result? All the previous stuff (√2, golden mean, etc) give the same results as before... but now π works.